The other day, while watching La Carte aux trésors at my elderly neighbor's house, I casually played peg solitaire on a board she has.
After many failures at trying to get rid of all pawns but one, I started to wonder about the mathematics & algorithmics behind that game...
Back home, I was astonished to discover that there is no solution to the European board with the initial hole centrally located! We could have been playing the game for a long, long time without knowing about this... I was also delighted to discovered Hans Zantema very elegant proof of this.
Actually, the European board can be beaten by slightly shifting the initial hole position:

That's when I decided to write a Python solver in order to beat the game!
And I ended up by producing those GIFs:
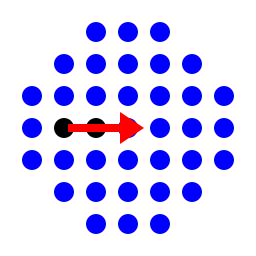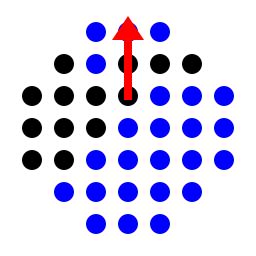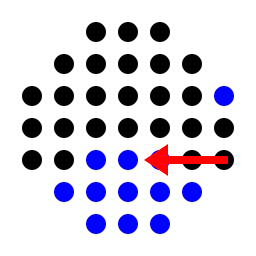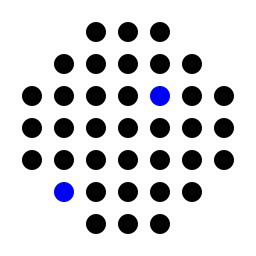
for the classic european board
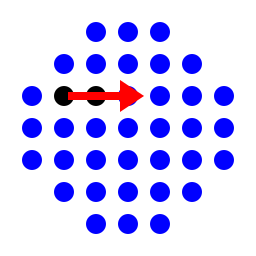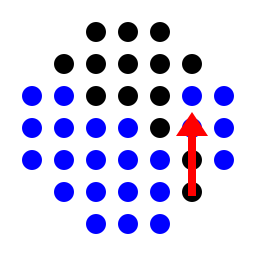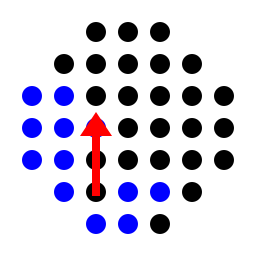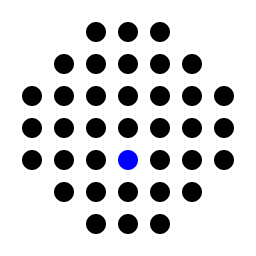
for the shifted european board
The source code can be found here: peg_solitaire_solver_gif.py. It is MIT licensed and the GIFs are under CC0.
The solver in itself is relatively simple, and the code not much worth commenting. I used Max Khrapov heuristic: without it, even while ignoring board symetries, I couldn't find a solution with less than 4 remaining pawns... Even after testing more than 10.000.000 board configurations! But now, it takes only a few seconds to complete on my computer.
The program relies on the gizeh & moviepy Pypi packages in order to generate the GIFs, but those dependencies are not needed by the solver.














