Dans le numéro 171 du magazine tangente, page 47, un intéressant petit problème mathématique est posé au lecteur.
Une jeune femme était en vacances au bord du lac Circulaire, un grand plan d’eau artificiel ainsi nommé pour sa forme circulaire précise. Pour échapper à un soupirant envahissant qui la harcelait, elle monta dans une barque et rama jusqu’à un radeau ancré au centre du lac. Son poursuivant décida de l’attendre sur le rivage, sachant qu’elle devrait revenir à terre. Il pouvait marcher quatre fois plus vite qu’elle pouvait ramer, et pensait pouvoir la joindre dès que son bateau toucherait le bord du lac. Mais la jeune femme, major de mathématiques au Radcliffe College et sportive de haut niveau, savait qu’une fois à terre, elle pourrait distancer le fâcheux. Il était seulement nécessaire de mettre au point une stratégie pour accoster à un point du rivage avant qu’il ne puisse y arriver. Elle trouva rapidement un plan assez simple. Quelle était la stratégie de la jeune femme ? On suppose qu’elle connaît à tout moment sa position exacte sur le lac.
Cependant, la solution proposée par tangente ne me satisfait pas vraiment. L'énoncé de la question laisse un peu de liberté d'interprétation, et la solution du magazine comporte, je crois, une petite incohérence.
Afin de visualiser les différentes solutions possibles selon les règles que l'on choisit de fixer, j'ai développé un petit simulateur web: https://chezsoi.org/lucas/maths/lady_of_the_lake.html (incluant la description de la solution de Tangente).
La configuration par défaut correspond à la solution de tangente :
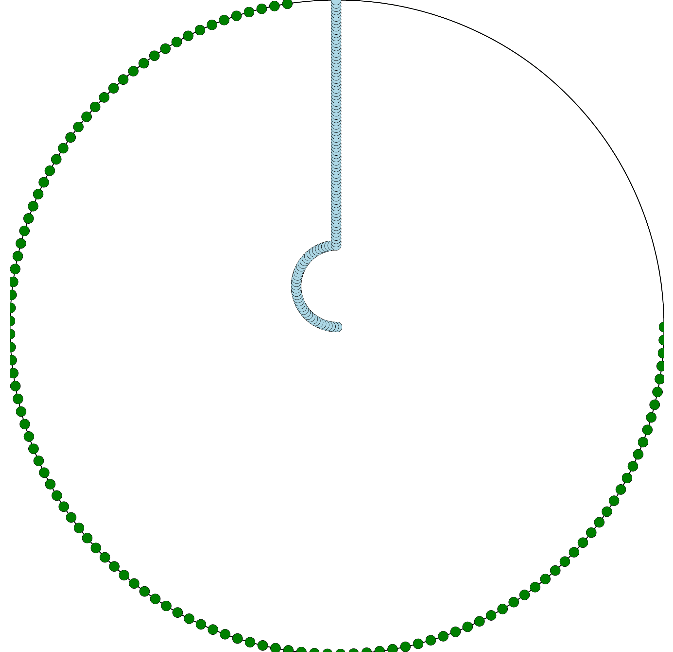
Cete solution prend comme postulat que la direction du soupirant est invariante, c'est-à-dire qu'il choisit une direction pour tourner autour du lac au départ, et qu'il n'en change jamais ensuite.
Néanmoins, avec un tel postulat, une solution bien plus simple est de prendre le soupirant à contre-pied :
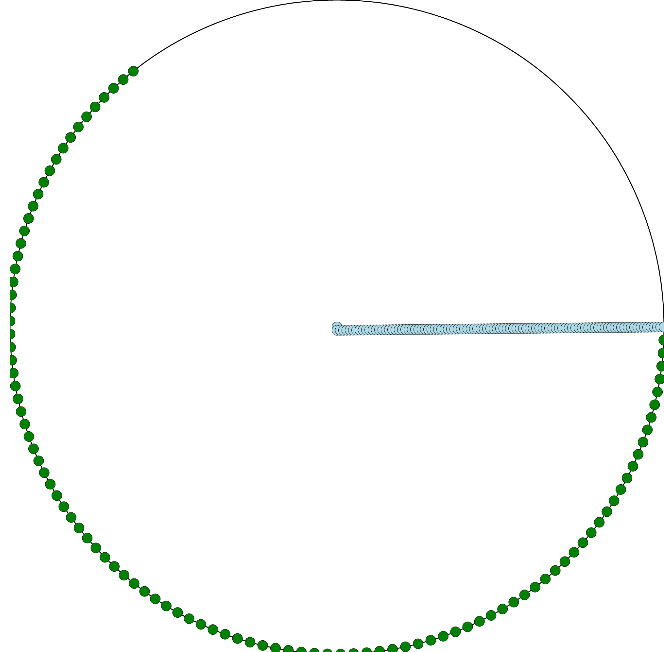
Au-contraire, si on considère que le poursuivant adapte sa direction afin de se rapprocher systématiquement de la lady, alors la solution de tangente ne fonctionne pas:
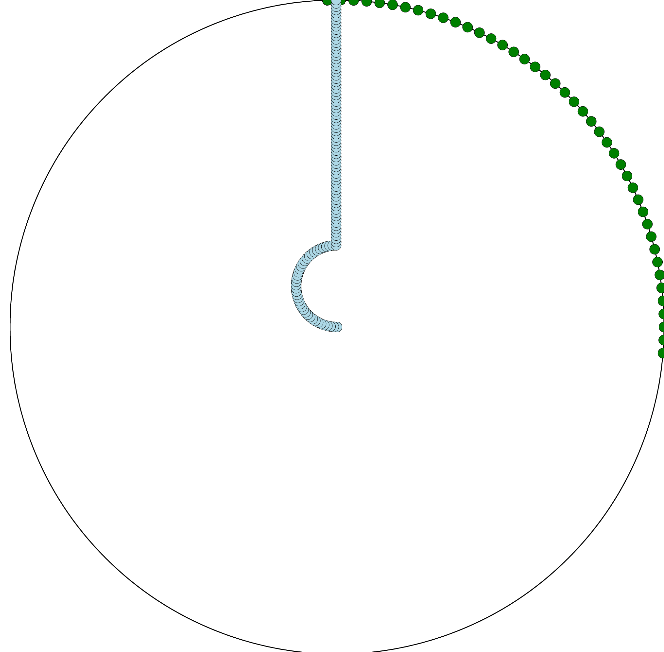
Essayons maintenant de simuler une lady qui s'adapte véritablement et dynamiquement à la position de son poursuivant,
"de sorte que le centre du lac soit toujours compris entre elle et son poursuivant sur le rivage, les trois points étant alignés", comme propose la solution de tangente :
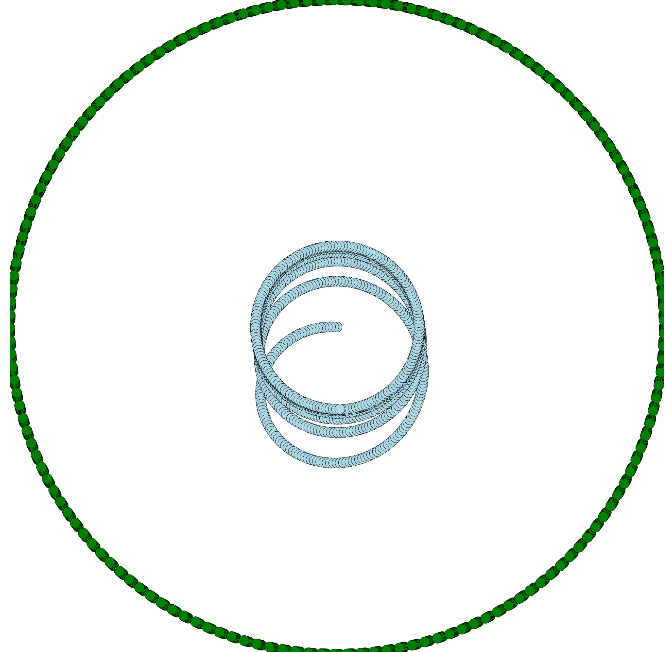
Que se passe-t-il ??
Avec un rapport de vitesses de 4, la lady ne peut pas échapper à son poursuivant. Elle est bloquée au centre du lac, sans pouvoir le prendre de vitesse. Il est intéressant de remarquer que sa trajectoire semble converger vers un cercle de rayon r / 4 (où r est le rayon du lac).
Enfin, on peut essayer des rapports de vitesses plus petits, pour essayer de déterminer quand il devient possible pour la lady de gagner.
Les valeurs obtenues avec le simulateur web sont sensibles au "pas" de simulation, mais avec un rapport de 3.6 on peut par exemple observer que la lady bat son poursuivant de vitesse :
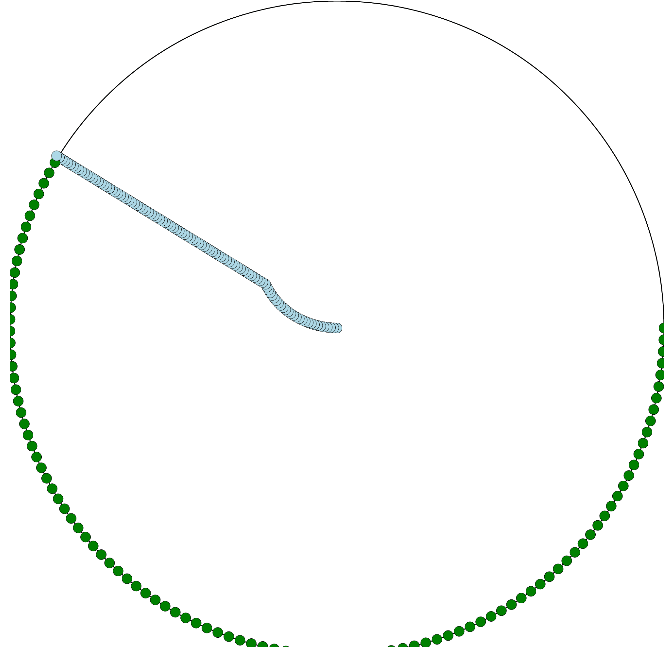
Qu'en pensez-vous ? N'hésitez pas à laisser votre avis sur ce problème en commentaire !
[EDIT 2019/06/15] le mois dernier la chaîne Youtube Numberphile a sorti une vidéo au sujet de ce problème : Game of Cat and Mouse. Le mathématicien Ben Sparks développe son raisonnement et démontre d'une part que j'avais tord, car il existe une solution, mais d'autre part que ce n'est pas celle de Tangente non plus ! Il existe en effet une zone circulaire où la lady peut progressivement se placer à l'opposé de son poursuivant, pour ensuite sprinter vers le rivage.
[EDIT 2022/10/25] : El Jj évoque ce problème dans l'une de se vidéos pour Mathctober, et le problème aurait été étudié par Leonard De Vinci :














