Hiding secret words in Sudokus with Python

🔗

Yesterday I was crafting some puzzles for my girlfriends, and I was looking for letter-based ones where I a secret word would be revealed once solved.

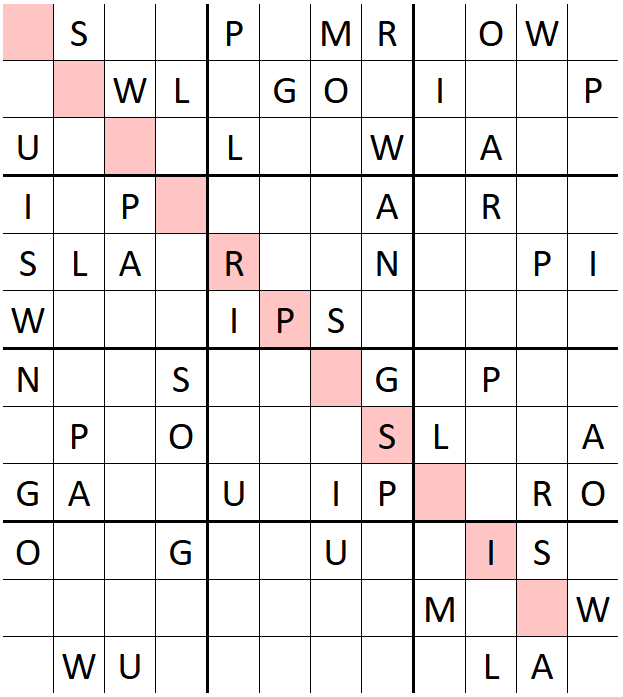
Solution of a size-12 Wordoku I created displaying the hidden words: AMOUR PASSION Wordoku initial grid for this same puzzle

With this same goal, I had already once worked on an open-source JS word search generator: https://lucas-c.github.io/wordfind/

(pour les francophones, vous trouverez quelques autres générateurs de jeux de lettres / chiffres dans cet article sur linuxfr.org)

This time I started crafting Masyu puzzles into letter shapes, but then I realized Sudokus would be a perfect pick, with digits replaced by letters ! Those are sometimes named Wordokus.

Hence I wrote a Wordoku generator in Python, where the secret word appears in the diagonal starting from the top-left: secret_word_sudokulike_grid_generator.py

# ./secret_word_sudokulike_grid_generator.py ensemble

   ..L.|...J               EMLS|BNKJ
   BNK.|...L               BNKJ|EMSL
   ---------               ---------
   ....|....               MLSB|JENK
   J..E|.S.M               JKNE|LSBM
   ---------   solution:   ---------
   S..K|....               SBJK|MLEN
   L..N|KB.S               LEMN|KBJS
   ---------               ---------
   .J.M|.KLB               NJEM|SKLB
   .S.L|..ME               KSBL|NJME

Because I wanted to be able to generate grids for any size, even for prime number sizes like 7, this program can drop the constraint of the boxes for those cases: the generated grid is a pseudo-sudoku, where the only rules are that columns & rows must contain all letters.

# ./secret_word_sudokulike_grid_generator.py --no-boxes-constraint ensemble

   E . M . . L . .               E D M S N L Q B
   . N . M . . S L               Q N D M B E S L
   B E . . . . . N               B E S L Q D M N
   . . . . . . . .   solution:   N S B E L Q D M
   D . L B . N . S               D Q L B M N E S
   . M E . . . N .               L M E D S B N Q
   S B . . E . . D               S B Q N E M L D
   . . . Q D S B .               M L N Q D S B E

You can see that the word ENSEMBLE appears on the diagonal in the solution.

On the technical side, the script is relatively straightforward. I only needed a fast sudoku solver. I used Ali Assaf's excellent one, that he describes in this article: https://www.cs.mcgill.ca/~aassaf9/python/algorithm_x.html

Using the fact that Sudoku puzzles may be described as an exact cover problem, he implemented Donald Knuth « Algorithm X » with Dancing Links ( how poetic ! )

Kudos to him for writing this. The code is under the GNU GPL license.

At some point I tried to optimize the code using Numpy & Numba, but I faced many issues with the later lib: no support for np.argwhere / np.setdiff1d / np.isin / np.in1d, new bugs... I started looking at at contributing by implementing those, but Numba's internal code is quite complex. 😞

In the end I did not bother improving the performances: even for a large grid like the size-12 one at the top of this article, the script execution times is between 10s and 10min, which is totally OK for my needs.

EDIT [2019/10/05]: I discovered that this lind of puzzle was sometimes called « SudoLettre » in French.

• • • • • • • • • •